Systematic Investor's Blog    About    Contact

Simulating correlated random walks with Copulas

16 Jan 2015

To install Systematic Investor Toolbox (SIT) please visit About page.

Another great article from mktstk: Simulating correlated random walks with Copulas

We can replicate this example using R

	#*****************************************************************
	# Load historical data
	#****************************************************************** 
	library(SIT)
	load.packages('quantmod')

filename = 'intraday.Rdata'
if(!file.exists(filename)) {
	data <- new.env()
		data$YHOO = getSymbol.intraday.google('YHOO', 'NASDAQ', 60, '15d')
		data$FB = getSymbol.intraday.google('FB', 'NASDAQ', 60, '15d')
	bt.prep(data, align='remove.na')
save(data, file=filename)
}
load(file=filename)

	#*****************************************************************
	# Generate simulations
	#****************************************************************** 
	prices = data$prices
 	n = ncol(prices)
	rets = diff(log(prices))
		rets = coredata(na.omit(rets))
 
 # Plot prices 
 matplot(exp(apply(rets,2,cumsum)), type='l', main='Actual Price path')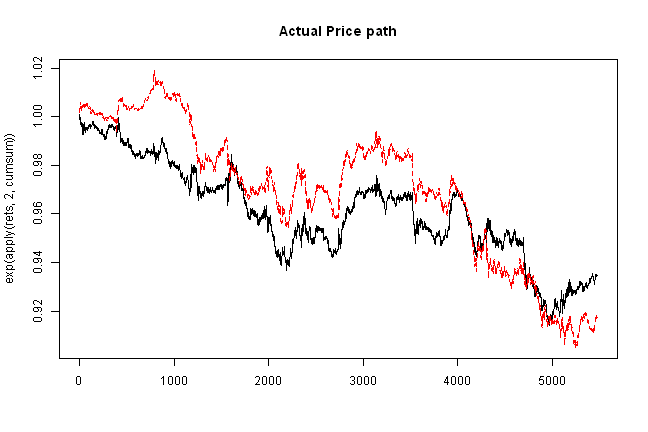

plot of chunk plot-2

# helper function to visualize distribution
visualize.rets = function(fit.sim) {
	labs = colnames(rets)
	xhist = hist(fit.sim[,1], plot=FALSE)
	yhist = hist(fit.sim[,2], plot=FALSE)

	top =max(c(xhist$counts, yhist$counts))

	layout(matrix(c(2,0,1,3),2,2,byrow=TRUE), c(3,1), c(1,3), TRUE)
 par(mar=c(3,3,1,1))
 plot(fit.sim[,1], fit.sim[,2], xlab=labs[1], ylab=labs[2], col='blue', las=1)
 
 par(mar=c(0,3,1,1))
	barplot(xhist$counts, axes=FALSE, ylim=c(0, top), space=0,col="light green") 

	barplot(yhist$counts, axes=FALSE, xlim=c(0, top), space=0, horiz=TRUE,col="light blue")
}


# Helper function to check Copula fit
copula.check = function(fit.sim) {
	# plot simulated vs actual
 labs = colnames(rets)
 layout(1)
	plot(rets[,1], rets[,2], xlab=labs[1], ylab=labs[2], col='blue', las=1)
	points(fit.sim[,1], fit.sim[,2], col='red')

	# compare stats for simulated vs actual
	temp = matrix(0,nr=5,nc=2)
 	colnames(temp) = spl('Actual,Simulated')
  rownames(temp) = c('Correlation', paste('Mean', labs), paste('StDev', labs))
 temp[1,] = c(cor(rets)[1,2], cor(fit.sim)[1,2])
 temp[2:3,] = 252 * cbind(apply(rets, 2, mean), apply(fit.sim, 2, mean))
 temp[4:5,] = sqrt(252) * cbind(apply(rets, 2, sd), apply(fit.sim, 2, sd))
 print(round(100*temp,2))               
 
 # check if returns come from same distributions
	for (i in 1:2) {
 	print(labs[i])
		print(ks.test(rets[,i], fit.sim[i]))
  }
  
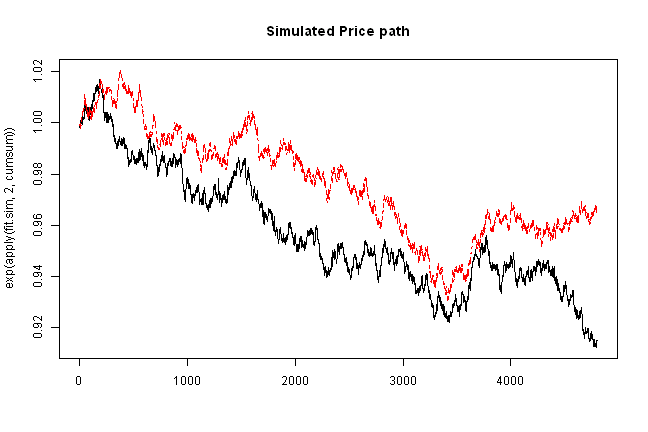
  # plot simulated price path
  matplot(exp(apply(fit.sim,2,cumsum)), type='l', main='Simulated Price path')
}


 # fit Copula
 load.packages('copula')

package ‘gsl’ successfully unpacked and MD5 sums checked package ‘ADGofTest’ successfully unpacked and MD5 sums checked package ‘stabledist’ successfully unpacked and MD5 sums checked package ‘mvtnorm’ successfully unpacked and MD5 sums checked package ‘pspline’ successfully unpacked and MD5 sums checked package ‘copula’ successfully unpacked and MD5 sums checked

The downloaded binary packages are in C:\Temp\RtmpCw8dcM\downloaded_packages

 gumbel.cop = gumbelCopula(dim=n)
 	uniform.data = pobs(rets)
 gumbel = fitCopula(gumbel.cop, uniform.data, method="ml")
	
 # create custom distribution by combining fitted margins with fitted copula
 margins=c("norm","norm")
 paramMargins=apply(rets,2,function(x) list(mean=mean(x), sd=sd(x)))
 
 fit = mvdc(copula = gumbelCopula(gumbel@estimate, dim=n),
		margins=margins,paramMargins=paramMargins)

	# simulate from fitted distn
	fit.sim = rMvdc(4800, fit)
 
 copula.check(fit.sim)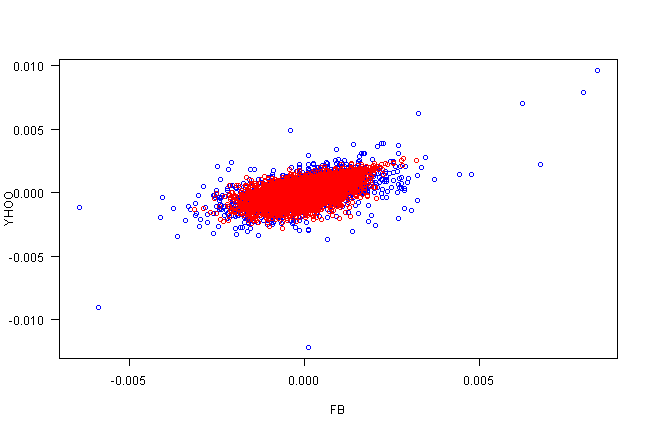

plot of chunk plot-2

  Actual Simulated
Correlation 57.13 57.38
Mean FB -0.31 -0.47
Mean YHOO -0.40 -0.17
StDev FB 1.24 1.25
StDev YHOO 1.23 1.23

FB


	Two-sample Kolmogorov-Smirnov test

data:  rets[, i] and fit.sim[i]
D = 0.9404, p-value = 0.3395
alternative hypothesis: two-sided

YHOO


	Two-sample Kolmogorov-Smirnov test

data:  rets[, i] and fit.sim[i]
D = 0.8792, p-value = 0.4222
alternative hypothesis: two-sided

plot of chunk plot-2

 visualize.rets(fit.sim)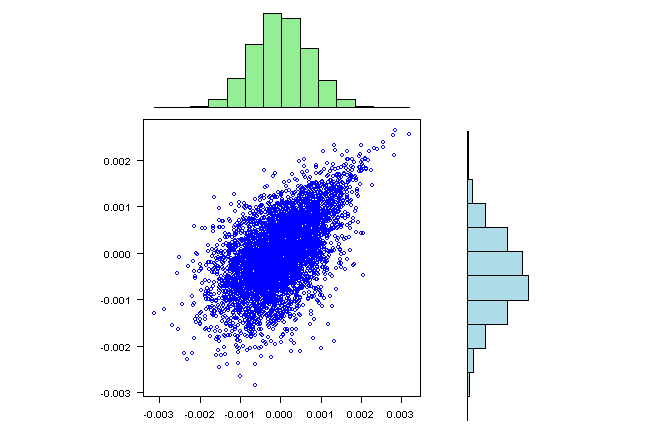

plot of chunk plot-2

	# alternatively we can do it by hand, please note to go from uniform data
 # to original data, we can use quantile function
 # i.e [simulation by inverse cdf](https://xianblog.wordpress.com/2015/01/14/simulation-by-inverse-cdf/)
 # qnorm(runif(10^8)) and rnorm(10^8) are equivalent
	uniform.sim = rCopula(4800, gumbelCopula(gumbel@estimate, dim=n))
	fit.sim2 = cbind(
		qnorm(uniform.sim[,1],mean(rets[,1]),sd(rets[,1])),
		qnorm(uniform.sim[,2],mean(rets[,2]),sd(rets[,2]))
	)

 copula.check(fit.sim2)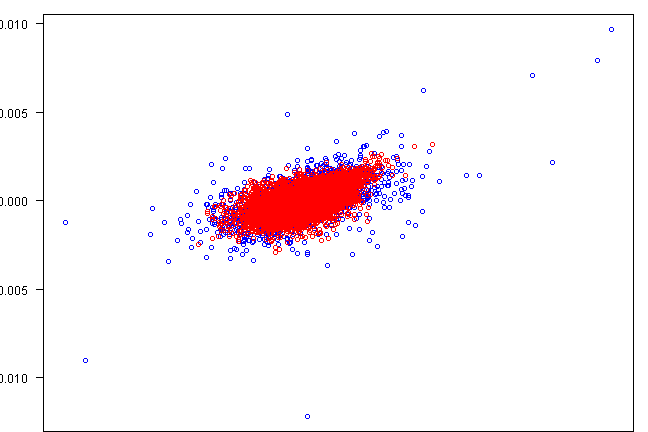

plot of chunk plot-2

  Actual Simulated
Correlation 57.13 57.14
Mean FB -0.31 -0.22
Mean YHOO -0.40 -0.56
StDev FB 1.24 1.24
StDev YHOO 1.23 1.21

FB


	Two-sample Kolmogorov-Smirnov test

data:  rets[, i] and fit.sim[i]
D = 0.7791, p-value = 0.5787
alternative hypothesis: two-sided

YHOO


	Two-sample Kolmogorov-Smirnov test

data:  rets[, i] and fit.sim[i]
D = 0.795, p-value = 0.5525
alternative hypothesis: two-sided

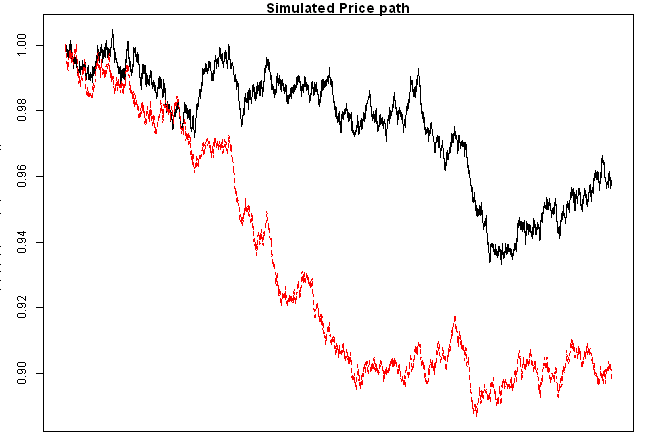
plot of chunk plot-2

 visualize.rets(fit.sim2)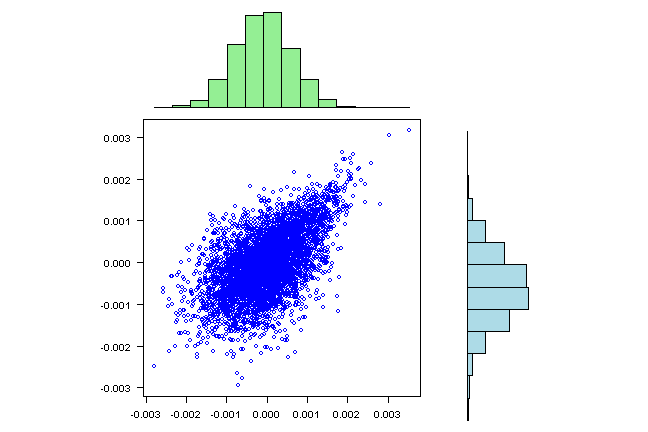

plot of chunk plot-2

	visualize.rets(rets)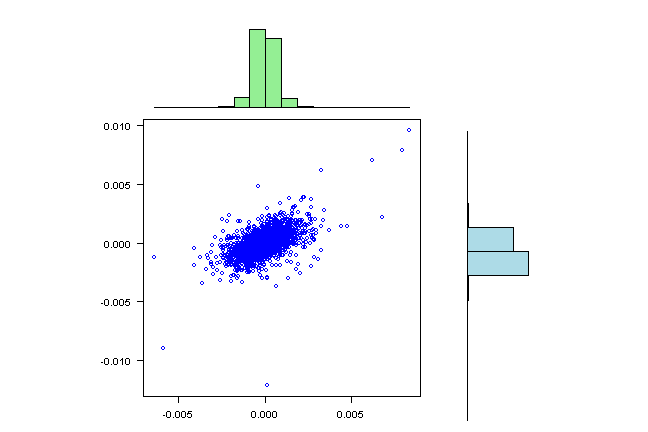

plot of chunk plot-2

Please note that Standard Deviation is huge relative to the Mean, which is close to zero; hence, we are very likely to get positive and negative outcomes in some cases.

For additional references on the topic, I found following references very useful:

(this report was produced on: 2015-01-17)

Related Posts