Exponentially Weighted Volatility using RCPP
10 Apr 2016To install Systematic Investor Toolbox (SIT) please visit About page.
The Exponentially Weighted Volatility is a measure of volatility that put more weight on the recent observations. We will use following formula to compute the Exponentially Weighted Volatility:
S[t]^2 = SUM (1-a) * a^i * (r[t-1-i] - rhat[t])^2, i=0 … inf
where rhat[t] is the corresponding the Exponentially Weighted mean
rhat[t] = SUM (1-a) * a^i * r[t-1-i], i=0 … inf
For reference on the computations of Exponentially Weighted Volatility please check:
The above formula depends on the full price history at each point in time and took a while to compute. Hence, I want to share how Rcpp and RcppParallel helped to reduce computation time.
I will use a historic dataset of the Foreign Exchange Rates as my testing data.
First we compute average rolling volatility
#*****************************************************************
# Compute Log Returns
#*****************************************************************
ret = diff(log(data$prices))
tic(5)
hist.vol = sqrt(252) * bt.apply.matrix(ret, runSD, n = 200)
toc(5)[1] “Elapsed time is 0.17 seconds\n”
Next, let’s code the Exponentially Weighted logic
# create RCPP functions to compute the Exponentially Weighted Volatility
load.packages('Rcpp')
sourceCpp(code='
#include <Rcpp.h>
using namespace Rcpp;
using namespace std;
// [[Rcpp::plugins(cpp11)]]
//ema[1] = 0
//ema[t] = (1-a)*r[t-1] + (1-a)*a*ema[t-1]
// [[Rcpp::export]]
NumericVector run_ema_cpp(NumericVector x, double ratio) {
auto sz = x.size();
NumericVector res(sz);
int t;
// find start index; first non NA item
for(t = 0; t < sz; t++) {
if(!NumericVector::is_na(x[t])) break;
res[t] = NA_REAL;
}
int start_t = t;
res[start_t] = 0;
for(t = start_t + 1; t < sz; t++) {
res[t] = (1-ratio) * ( x[t-1] + ratio * res[t-1]);
}
return res;
}
//sigma[1] = 0
//sigma[t] = SUM (1-a) * a^i * (r[t-1-i] - rhat[t])^2, i=0 ... inf
// [[Rcpp::export]]
NumericVector run_esd_cpp(NumericVector x, double ratio) {
auto sz = x.size();
NumericVector res(sz);
int t;
// find start index; first non NA item
for(t = 0; t < sz; t++) {
if(!NumericVector::is_na(x[t])) break;
res[t] = NA_REAL;
}
int start_t = t;
double ema = 0;
res[start_t] = 0;
for(t = start_t + 1; t < sz; t++) {
ema = (1-ratio) * ( x[t-1] + ratio * ema);
double sigma = 0;
for(int i = 0; i < (t - start_t); i++) {
sigma += pow(ratio,i) * pow(x[t-1-i] - ema, 2);
}
res[t] = (1-ratio) * sigma;
}
return res;
}
'
)
run.ema = function(x, n, ratio = n/(n+1)) run_ema_cpp(x, ratio)
run.esd = function(x, n, ratio = n/(n+1)) sqrt(run_esd_cpp(x, ratio))
tic(5)
hist.vol.exp = sqrt(252) * bt.apply.matrix(ret, run.esd, n = 60)
toc(5)[1] “Elapsed time is 106.16 seconds\n”
It took a while to execute this code. Fortunately, the code can easily run in parallel. Following is the RcppParallel version.
# create RCPP Parallel function to compute the Exponentially Weighted Volatility
load.packages('RcppParallel')
sourceCpp(code='
#include <Rcpp.h>
using namespace Rcpp;
using namespace std;
// [[Rcpp::plugins(cpp11)]]
// [[Rcpp::depends(RcppParallel)]]
#include <RcppParallel.h>
using namespace RcppParallel;
struct run_esd_helper : public Worker {
// input matrix to read from
const RMatrix<double> mat;
// internal variables
const double ratio;
const int nperiod;
// output matrix to write to
RMatrix<double> rmat;
// initialize from Rcpp input and output matrixes
run_esd_helper(const NumericMatrix& mat, double ratio, int nperiod, NumericMatrix rmat)
: mat(mat), ratio(ratio), nperiod(nperiod), rmat(rmat) { }
// main entry -function call operator that work for the specified range (begin/end)
void operator()(size_t begin, size_t end) {
for (size_t c1 = begin; c1 < end; c1++) {
int t;
// find start index; first non NA item
for(t = 0; t < nperiod; t++) {
if(!NumericVector::is_na(mat(t, c1))) break;
rmat(t,c1) = NA_REAL;
}
int start_t = t;
double ema = 0;
rmat(start_t, c1) = 0;
for(t = start_t + 1; t < nperiod; t++) {
ema = (1-ratio) * ( mat(t-1,c1) + ratio * ema);
double sigma = 0;
for(int i = 0; i < (t - start_t); i++) {
sigma += pow(ratio,i) * pow(mat(t-1-i,c1) - ema, 2);
}
rmat(t,c1) = (1-ratio) * sigma;
}
}
}
};
// [[Rcpp::export]]
NumericMatrix run_esd_parallel(NumericMatrix mat, double ratio) {
// allocate the matrix we will return
int nc = mat.ncol();
int nperiod = mat.nrow();
NumericMatrix rmat(nperiod, nc);
// parallel run
run_esd_helper p(mat, ratio, nperiod, rmat);
parallelFor(0, nc, p);
return rmat;
}
'
)
run.esd.parallel = function(x, n, ratio = n/(n+1)) { temp=x; x[]=sqrt(run_esd_parallel(x, ratio)); return(x) }
tic(5)
hist.vol.parallel = sqrt(252) * run.esd.parallel(ret, n = 60)
toc(5)[1] “Elapsed time is 14.65 seconds\n”
Great, the running time is more reasonable. Next let’s visualize the impact of using the Exponentially Weighted Volatility
dates = '2007::2010'
layout(1:2)
plota(ret[dates,1],type='h', col='black', plotX=F)
plota.legend(paste('Daily Log Returns for',names(ret)[1]), 'black')
plota(hist.vol.parallel[dates,1],type='l',col='black')
plota.lines(hist.vol[dates,1], col='blue')
plota.legend('Exponentially Weighted Volatility,Equal Weighted Annualized Volatility','black,blue')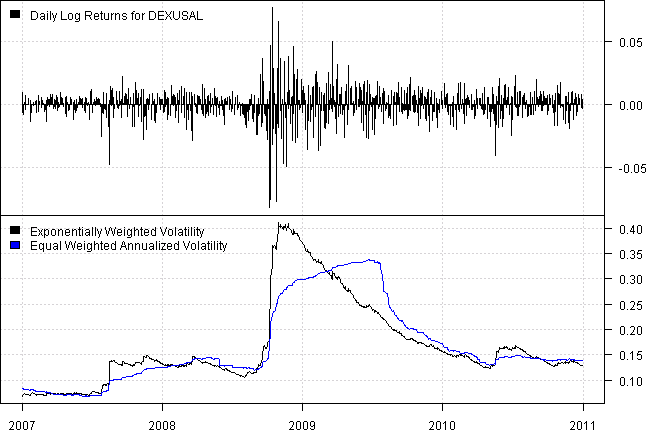
As expected, the Exponentially Weighted Volatility puts more weight on most recent observations and is a more reactive risk measure.
For your convenience, the 2016-04-10-Exponentially-Weighted-Volatility-RCPP post source code.