Review of Momentum and Markowitz A Golden Combination paper
04 Jun 2015To install Systematic Investor Toolbox (SIT) please visit About page.
The Momentum and Markowitz: A Golden Combination (2015) by Keller, Butler, Kipnis paper is a review of practitioner’s tools to make mean variance optimization portfolio a viable solution. In particular, authors suggest and test:
- adding maximum weight limits and
- adding target volatility constraint
to control solution of mean variance optimization.
Below I will have a look at the results for the 8 asset universe:
- S&P 500
- EAFE
- Emerging Markets
- US Technology Sector
- Japanese Equities
- 10-Year Treasuries
- T-Bills
- High Yield Bonds
First, let’s load historical data for all assets
#*****************************************************************
# Load historical data
#*****************************************************************
library(SIT)
load.packages('quantmod')
# load saved Proxies Raw Data, data.proxy.raw
# please see http://systematicinvestor.github.io/Data-Proxy/ for more details
load('data/data.proxy.raw.Rdata')
N8.tickers = '
US.EQ = VTI + VTSMX + VFINX
EAFE = EFA + VDMIX + VGTSX
EMER.EQ = EEM + VEIEX
TECH.EQ = QQQ + ^NDX
JAPAN.EQ = EWJ + FJPNX
MID.TR = IEF + VFITX
US.CASH = BIL + TB3M,
US.HY = HYG + VWEHX
'
data = env()
getSymbols.extra(N8.tickers, src = 'yahoo', from = '1970-01-01', env = data, raw.data = data.proxy.raw, set.symbolnames = T, auto.assign = T)
for(i in data$symbolnames) data[[i]] = adjustOHLC(data[[i]], use.Adjusted=T)
bt.prep(data, align='remove.na', fill.gaps = T)Next, let’s test the functionality of kellerCLAfun from Appendix A
#*****************************************************************
# Run tests, monthly data - works
#*****************************************************************
data = bt.change.periodicity(data, periodicity = 'months')
plota.matplot(scale.one(data$prices))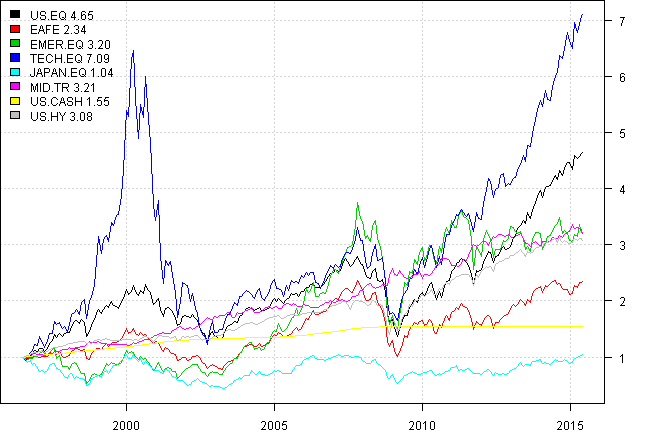
prices = data$prices
res = kellerCLAfun(prices, returnWeights = T, 0.25, 0.1, c('US.CASH', 'MID.TR'))
plotbt.transition.map(res[[1]]['2013::'])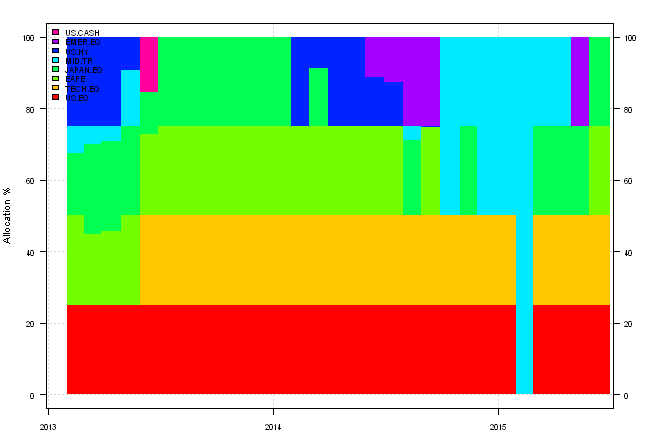
plota(cumprod(1 + res[[2]]), type='l')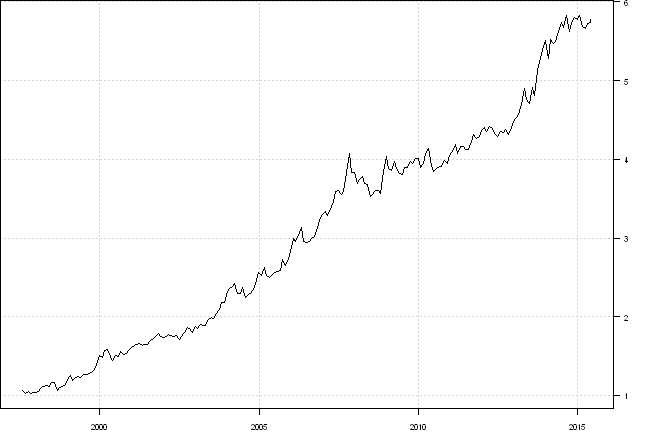
Next, let’s create a benchmark and set up commision structure to be used for all tests.
#*****************************************************************
# Create a benchmark
#*****************************************************************
models = list()
commission = list(cps = 0.01, fixed = 10.0, percentage = 0.0)
data$weight[] = NA
data$weight$US.EQ = 1
data$weight[1:12,] = NA
models$US.EQ = bt.run.share(data, clean.signal=T, commission=commission, trade.summary=T, silent=T)Next, let’s take weights from the kellerCLAfun and use them to create a back-test
#*****************************************************************
# transform kellerCLAfun into model results
#*****************************************************************
#models$CLA = list(weight = res[[1]], ret = res[[2]], equity = cumprod(1 + res[[2]]), type = "weight")
obj = list(weights = list(CLA = res[[1]]), period.ends = index(res[[1]]))
models = c(models, create.strategies(obj, data, commission=commission, trade.summary=T, silent=T)$models)We can easily replicate same results with base SIT functionality
#*****************************************************************
# Replicate using base SIT functionality
#*****************************************************************
weight.limit = data.frame(last(prices))
weight.limit[] = 0.25
weight.limit$US.CASH = weight.limit$MID.TR = 1
obj = portfolio.allocation.helper(data$prices,
periodicity = 'months', lookback.len = 12, silent=T,
const.ub = weight.limit,
create.ia.fn = function(hist.returns, index, nperiod) {
ia = create.ia(hist.returns, index, nperiod)
ia$expected.return = (last(hist.returns,1) + colSums(last(hist.returns,3)) +
colSums(last(hist.returns,6)) + colSums(last(hist.returns,12))) / 22
ia
},
min.risk.fns = list(
TRISK = target.risk.portfolio(target.risk = 0.1, annual.factor=12)
)
)
models = c(models, create.strategies(obj, data, commission=commission, trade.summary=T, silent=T)$models)Another idea is to use Pierre Chretien’s Averaged Input Assumptions
#*****************************************************************
# Let's use Pierre's Averaged Input Assumptions
#*****************************************************************
obj = portfolio.allocation.helper(data$prices,
periodicity = 'months', lookback.len = 12, silent=T,
const.ub = weight.limit,
create.ia.fn = create.ia.averaged(c(1,3,6,12), 0),
min.risk.fns = list(
TRISK.AVG = target.risk.portfolio(target.risk = 0.1, annual.factor=12)
)
)
models = c(models, create.strategies(obj, data, commission=commission, trade.summary=T, silent=T)$models)Finally we are ready to look at the results
#*****************************************************************
# Plot back-test
#*****************************************************************
models = bt.trim(models)
#strategy.performance.snapshoot(models, T)
plotbt(models, plotX = T, log = 'y', LeftMargin = 3, main = NULL)
mtext('Cumulative Performance', side = 2, line = 1)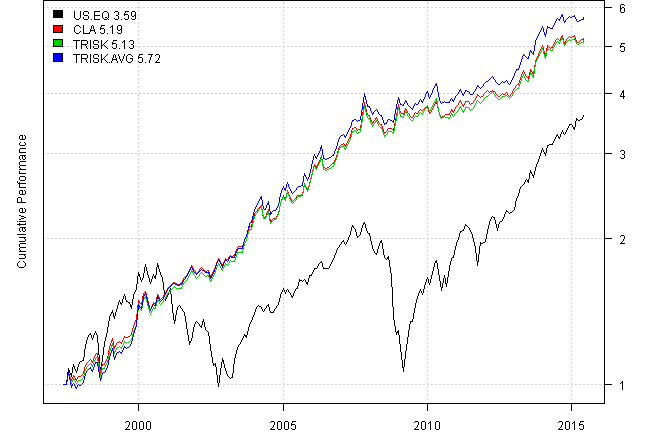
print(plotbt.strategy.sidebyside(models, make.plot=F, return.table=T, perfromance.fn=engineering.returns.kpi)) | US.EQ | CLA | TRISK | TRISK.AVG | |
|---|---|---|---|---|
| Period | May1997 - Jun2015 | May1997 - Jun2015 | May1997 - Jun2015 | May1997 - Jun2015 |
| Cagr | 7.36 | 9.57 | 9.49 | 10.16 |
| Sharpe | 0.53 | 1.02 | 1.01 | 1.04 |
| DVR | 0.33 | 1 | 0.98 | 1.01 |
| R2 | 0.63 | 0.98 | 0.97 | 0.97 |
| Volatility | 15.84 | 9.32 | 9.42 | 9.72 |
| MaxDD | -50.84 | -13.65 | -13.65 | -13.65 |
| Exposure | 99.08 | 99.08 | 99.08 | 99.08 |
| Win.Percent | 100 | 64.57 | 59.85 | 59.28 |
| Avg.Trade | 259.48 | 0.26 | 0.18 | 0.19 |
| Profit.Factor | NaN | 1.93 | 1.87 | 1.93 |
| Num.Trades | 1 | 717 | 1066 | 1051 |
layout(1)
barplot.with.labels(sapply(models, compute.turnover, data), 'Average Annual Portfolio Turnover') 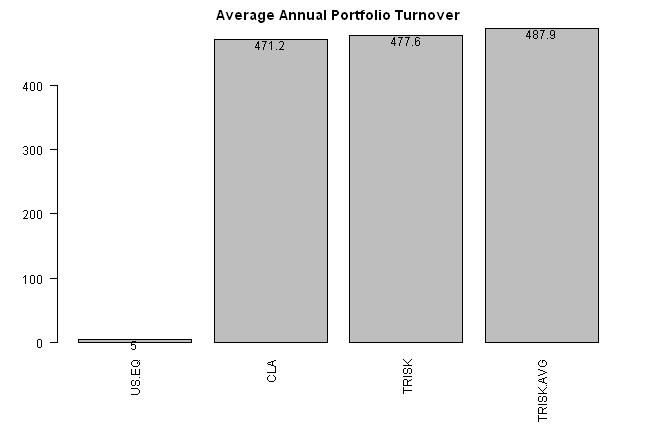
Our replication results are almost identical results to the results using kellerCLAfun.
Using Averaged Input Assumptions produces slightly better results.
I guess the main point that a reader should remember from reading Momentum and Markowitz: A Golden Combination (2015) by Keller, Butler, Kipnis paper is that it is a bad idea to blindly use the optimizer. Instead, you should apply common sense heuristics mentioned in the paper to make solution robust across time and various universes.
Supporting functions:
#*****************************************************************
# Appendix B. CLA code (in R) by Ilya Kipnis (QuantStratTradeR10) SSRN-id2606884.pdf
#*****************************************************************
require(quantmod)
require(PerformanceAnalytics)
require(TTR)
CCLA <- function(covMat, retForecast, maxIter = 1000,
verbose = FALSE, scale = 252,
weightLimit = .7, volThresh = .1)
{
if(length(retForecast) > length(unique(retForecast))) {
sequentialNoise <- seq(1:length(retForecast)) * 1e-12
retForecast <- retForecast + sequentialNoise
}
#initialize original out/in/up status
if(length(weightLimit) == 1) {
weightLimit <- rep(weightLimit, ncol(covMat))
}
# sort return forecasts
rankForecast <- length(retForecast) - rank(retForecast) + 1
remainingWeight <- 1 #have 100% of weight to allocate
upStatus <- inStatus <- rep(0, ncol(covMat))
i <- 1
# find max return portfolio
while(remainingWeight > 0) {
securityLimit <- weightLimit[rankForecast == i]
if(securityLimit < remainingWeight) {
upStatus[rankForecast == i] <- 1 #if we can't invest all remaining weight into the security
remainingWeight <- remainingWeight - securityLimit
} else {
inStatus[rankForecast == i] <- 1
remainingWeight <- 0
}
i <- i + 1
}
#initial matrices (W, H, K, identity, negative identity)
covMat <- as.matrix(covMat)
retForecast <- as.numeric(retForecast)
init_W <- cbind(2*covMat, rep(-1, ncol(covMat)))
init_W <- rbind(init_W, c(rep(1, ncol(covMat)), 0))
H_vec <- c(rep(0, ncol(covMat)), 1)
K_vec <- c(retForecast, 0)
negIdentity <- -1*diag(ncol(init_W))
identity <- diag(ncol(init_W))
matrixDim <- nrow(init_W)
weightLimMat <- matrix(rep(weightLimit, matrixDim), ncol=ncol(covMat), byrow=TRUE)
#out status is simply what isn't in or up
outStatus <- 1 - inStatus - upStatus
#initialize expected volatility/count/turning points data structure
expVol <- Inf
lambda <- 100
count <- 0
turningPoints <- list()
while(lambda > 0 & count < maxIter) {
#old lambda and old expected volatility for use with numerical algorithms
oldLambda <- lambda
oldVol <- expVol
count <- count + 1
#compute W, A, B
inMat <- matrix(rep(c(inStatus, 1), matrixDim), nrow = matrixDim, byrow = TRUE)
upMat <- matrix(rep(c(upStatus, 0), matrixDim), nrow = matrixDim, byrow = TRUE)
outMat <- matrix(rep(c(outStatus, 0), matrixDim), nrow = matrixDim, byrow = TRUE)
W <- inMat * init_W + upMat * identity + outMat * negIdentity
inv_W <- solve(W)
modified_H <- H_vec - rowSums(weightLimMat* upMat[,-matrixDim] * init_W[,-matrixDim])
A_vec <- inv_W %*% modified_H
B_vec <- inv_W %*% K_vec
#remove the last elements from A and B vectors
truncA <- A_vec[-length(A_vec)]
truncB <- B_vec[-length(B_vec)]
#compute in Ratio (aka Ratio(1) in Kwan.xls)
inRatio <- rep(0, ncol(covMat))
inRatio[truncB > 0] <- -truncA[truncB > 0]/truncB[truncB > 0]
#compute up Ratio (aka Ratio(2) in Kwan.xls)
upRatio <- rep(0, ncol(covMat))
upRatioIndices <- which(inStatus==TRUE & truncB < 0)
if(length(upRatioIndices) > 0) {
upRatio[upRatioIndices] <- (weightLimit[upRatioIndices] - truncA[upRatioIndices]) / truncB[upRatioIndices]
}
#find lambda -- max of up and in ratios
maxInRatio <- max(inRatio)
maxUpRatio <- max(upRatio)
lambda <- max(maxInRatio, maxUpRatio)
#compute new weights
wts <- inStatus*(truncA + truncB * lambda) + upStatus * weightLimit + outStatus * 0
#compute expected return and new expected volatility
expRet <- t(retForecast) %*% wts
expVol <- sqrt(wts %*% covMat %*% wts) * sqrt(scale)
#create turning point data row and append it to turning points
turningPoint <- cbind(count, expRet, lambda, expVol, t(wts))
colnames(turningPoint) <- c("CP", "Exp. Ret.", "Lambda", "Exp. Vol.", colnames(covMat))
turningPoints[[count]] <- turningPoint
#binary search for volatility threshold -- if the first iteration is lower than the threshold,
#then immediately return, otherwise perform the binary search until convergence of lambda
if(oldVol == Inf & expVol < volThresh) {
turningPoints <- do.call(rbind, turningPoints)
threshWts <- tail(turningPoints, 1)
return(list(turningPoints, threshWts))
} else if(oldVol > volThresh & expVol < volThresh) {
upLambda <- oldLambda
dnLambda <- lambda
meanLambda <- (upLambda + dnLambda)/2
while(upLambda - dnLambda > .00001) {
#compute mean lambda and recompute weights, expected return, and expected vol
meanLambda <- (upLambda + dnLambda)/2
wts <- inStatus*(truncA + truncB * meanLambda) + upStatus * weightLimit + outStatus * 0
expRet <- t(retForecast) %*% wts
expVol <- sqrt(wts %*% covMat %*% wts) * sqrt(scale)
#if new expected vol is less than threshold, mean becomes lower bound
#otherwise, it becomes the upper bound, and loop repeats
if(expVol < volThresh) {
dnLambda <- meanLambda
} else {
upLambda <- meanLambda
}
}
#once the binary search completes, return those weights, and the corner points
#computed until the binary search. The corner points aren't used anywhere, but they're there.
threshWts <- cbind(count, expRet, meanLambda, expVol, t(wts))
colnames(turningPoint) <- colnames(threshWts) <- c("CP", "Exp. Ret.", "Lambda", "Exp. Vol.", colnames(covMat))
turningPoints[[count]] <- turningPoint
turningPoints <- do.call(rbind, turningPoints)
return(list(turningPoints, threshWts))
}
#this is only run for the corner points during which binary search doesn't take place
#change status of security that has new lambda
if(maxInRatio > maxUpRatio) {
inStatus[inRatio == maxInRatio] <- 1 - inStatus[inRatio == maxInRatio]
upStatus[inRatio == maxInRatio] <- 0
} else {
upStatus[upRatio == maxUpRatio] <- 1 - upStatus[upRatio == maxUpRatio]
inStatus[upRatio == maxUpRatio] <- 0
}
outStatus <- 1 - inStatus - upStatus
}
#we only get here if the volatility threshold isn't reached
#can actually happen if set sufficiently low
turningPoints <- do.call(rbind, turningPoints)
threshWts <- tail(turningPoints, 1)
return(list(turningPoints, threshWts))
}
sumIsNa <- function(column) {
return(sum(is.na(column)))
}
returnForecast <- function(prices) {
forecast <- (ROC(prices, n = 1, type="discrete") + ROC(prices, n = 3, type="discrete") +
ROC(prices, n = 6, type="discrete") + ROC(prices, n = 12, type="discrete"))/22
forecast <- as.numeric(tail(forecast, 1))
return(forecast)
}
kellerCLAfun <- function(prices, returnWeights = FALSE,
weightLimit, volThresh, uncappedAssets)
{
if(sum(colnames(prices) %in% uncappedAssets) == 0) {
stop("No assets are uncapped.")
}
#initialize data structure to contain our weights
weights <- list()
#compute returns
returns <- Return.calculate(prices)
returns[1,] <- 0 #impute first month with zeroes
ep <- endpoints(returns, on = "months")
for(i in 2:(length(ep) - 12)) {
priceSubset <- prices[ep[i]:ep[i+12]] #subset prices
retSubset <- returns[ep[i]:ep[i+12]] #subset returns
assetNAs <- apply(retSubset, 2, sumIsNa)
zeroNAs <- which(assetNAs == 0)
priceSubset <- priceSubset[, zeroNAs]
retSubset <- retSubset[, zeroNAs]
#remove perfectly correlated assets
retCors <- cor(retSubset)
diag(retCors) <- NA
corMax <- round(apply(retCors, 2, max, na.rm = TRUE), 7)
while(max(corMax) == 1) {
ones <- which(corMax == 1)
valid <- which(!names(corMax) %in% uncappedAssets)
toRemove <- intersect(ones, valid)
toRemove <- max(valid)
retSubset <- retSubset[, -toRemove]
priceSubset <- priceSubset[, -toRemove]
retCors <- cor(retSubset)
diag(retCors) <- NA
corMax <- round(apply(retCors, 2, max, na.rm = TRUE), 7)
}
covMat <- cov(retSubset) #compute covariance matrix
#Dr. Keller's return forecast
retForecast <- returnForecast(priceSubset)
uncappedIndex <- which(colnames(covMat) %in% uncappedAssets)
weightLims <- rep(weightLimit, ncol(covMat))
weightLims[uncappedIndex] <- 1
cla <- CCLA(covMat = covMat, retForecast = retForecast, scale = 12,
weightLimit = weightLims, volThresh = volThresh) #run CCLA algorithm
CPs <- cla[[1]] #corner points
wts <- cla[[2]] #binary search volatility targeting -- change this line and the next
#if using max sharpe ratio golden search
wts <- wts[, 5:ncol(wts)] #from 5th column to the end
if(length(wts) == 1) {
names(wts) <- colnames(covMat)
}
zeroes <- rep(0, ncol(prices) - length(wts))
names(zeroes) <- colnames(prices)[!colnames(prices) %in% names(wts)]
wts <- c(wts, zeroes)
wts <- wts[colnames(prices)]
#append to weights
wts <- xts(t(wts), order.by=tail(index(retSubset), 1))
weights[[i]] <- wts
}
weights <- do.call(rbind, weights)
#compute strategy returns
stratRets <- Return.portfolio(returns, weights = weights)
if(returnWeights) {
return(list(weights, stratRets))
}
return(stratRets)
}(this report was produced on: 2015-06-04)