Optimizing Run Time for Large Universe
22 Apr 2015To install Systematic Investor Toolbox (SIT) please visit About page.
Recently, I was asked if Systematic Investor Toolbox (SIT) back-testing framework is suitable for running large universe back-tests.
Below, I will present the steps I took to test and optimize the running time. I will base this experiment on the Volatility Quantiles post i wrote back in 2012.
First, let’s generate 10 years of daily data for 25,000 securities.
Please note that this code requires lot’s of memory to store results;
hence, you might want to add --max-mem-size=8000M to your R parameters.
# https://systematicinvestor.wordpress.com/2012/06/05/volatility-quantiles/
#*****************************************************************
# Load historical data
#*****************************************************************
library(SIT)
load.packages('quantmod')
tic(11)
tic(1)
n = 25 * 1000
nperiods = 10 * 252
# force high vol to small return
library(MASS)
mu = c(5,20) / 100
sigma = c(5,10) / 100
rho = -0.9
cov.matrix = sigma%*%t(sigma) * matrix(c(1,rho,rho,1),2,2)
temp = mvrnorm(n, mu, cov.matrix)
mu = temp[,1]
sigma = temp[,2]
sigma[sigma < 1/100] = 1/100
ret = matrix(rnorm(n*nperiods), nr=n)
ret = t(ret * sigma/sqrt(252) + mu/252)
#colnames(ret) = paste('A',1:n)
dates = seq(Sys.Date()-nperiods+1, Sys.Date(), 1)
#prices = bt.apply.matrix(1 + ret, cumprod)
#plot(prices[,1])
#data = env(
# symbolnames = colnames(prices)
# dates = dates
# fields = 'Cl'
# Cl = prices)
#bt.prep.matrix(data)Next I tried to run the original code from the Volatility Quantiles post and eventually run out of memory.
Below i modified original code to make it work.
#*****************************************************************
# Create Quantiles based on the historical one year volatility
#******************************************************************
period.ends = endpoints(dates, 'weeks')
period.ends = period.ends[period.ends > 0]
tic(2)
tic(1)
# compute historical one year volatility
sd252 = bt.apply.matrix(ret, runSD, 252)
toc(1); tic(1)Elapsed time is 48.12 seconds
# split stocks into Quantiles using one year historical Volatility
n.quantiles=5
start.t = which(period.ends >= (252+2))[1]
quantiles = weights = ret[period.ends,] * NA
for( t in start.t:len(period.ends) ) {
i = period.ends[t]
factor = sd252[i,]
ranking = ceiling(n.quantiles * rank(factor, na.last = 'keep','first') / count(factor))
quantiles[t,] = ranking
weights[t,] = 1/tapply(rep(1,n), ranking, sum)[ranking]
}
# free memory
env.del(spl('prices,sd252'), globalenv())
gc(T) used (Mb) gc trigger (Mb) max used (Mb) Ncells 561806 30.1 984024 52.6 984024 52.6 Vcells 81877454 624.7 199500757 1522.1 199499815 1522.1
#*****************************************************************
# Create backtest for each Quintile
#******************************************************************
toc(1); tic(1)Elapsed time is 10.63 seconds
models = list()
quantiles = ifna(quantiles,0)
for( i in 1:n.quantiles) {
temp = weights * NA
temp[] = 0
temp[quantiles == i] = weights[quantiles == i]
weight = ret * NA
weight[period.ends,] = temp
weight = ifna(apply(mlag(weight), 2, ifna.prev),0)
rets = rowSums(ret * weight)
models[[ paste('Q',i,sep='_') ]] = list(
ret = make.xts(rets, dates),
equity = make.xts(cumprod(1 + rets),dates))
}
toc(1)Elapsed time is 50.27 seconds
toc(2) Elapsed time is 109.02 seconds
Looking at the timing, there are 2 bottle necks:
- computation of historical one year volatility
- creating back-test for each quantile
To address running time for computation of historical one year volatility, I tried following approaches:
# Run Cluster
load.packages('parallel')
tic(2)
tic(1)
cl = setup.cluster(NULL, 'ret',envir=environment())
toc(1); tic(1)Elapsed time is 19.56 seconds
out = clusterApplyLB(cl, 1:n, function(i) { runSD(ret[,i], 252) } )
toc(1); tic(1)Elapsed time is 17.43 seconds
stopCluster(cl)
sd252 = do.call(c, out)
dim(sd252) = dim(ret)
toc(1)Elapsed time is 0.54 seconds
toc(2) Elapsed time is 37.67 seconds
Not much faster, it takes almost 19 seconds to move large ret matrix around.
Next I looked at RcppParallel for help.
#include <Rcpp.h>
using namespace Rcpp;
using namespace std;
// [[Rcpp::plugins(cpp11)]]
// [[Rcpp::depends(RcppParallel)]]
#include <RcppParallel.h>
using namespace RcppParallel;
//[Standard deviation](http://mathforum.org/library/drmath/view/71724.html)
// sqrt((sX2 - sX^2/n)/(n-1))
struct run_sd_helper : public Worker {
// input matrix to read from
const RMatrix<double> mat;
// internal variables
int rstart, rend;
const int nwindow, nwindow1;
RVector<double> sum, sum2;
// output matrix to write to
RMatrix<double> rmat;
// flag to indicate initialization
bool first_run;
// initialize from Rcpp input and output matrixes
run_sd_helper(const NumericMatrix& mat, int rstart, int rend,
NumericVector sum, NumericVector sum2, NumericMatrix rmat)
: mat(mat), rstart(rstart), rend(rend), nwindow(rend - rstart), nwindow1(nwindow-1),
sum(sum), sum2(sum2), rmat(rmat), first_run(true) { }
// helper function to shift one period in time
void update(int i) {
rstart = i;
rend = rstart + nwindow;
first_run = false;
}
// do initialization, pre-compute sum and sum2
void do_first_run(size_t begin, size_t end) {
for (size_t c1 = begin; c1 < end; c1++) {
double dsum, dsum2;
dsum = dsum2 = 0;
for (int r = rstart; r < rend; r++) {
double d = mat(r, c1);
dsum += d;
dsum2 += pow(d, 2);
}
sum[c1] = dsum;
sum2[c1] = dsum2;
rmat(rend - 1, c1) = sqrt((dsum2 - pow(dsum, 2) / nwindow) / nwindow1);
}
}
// do incremental update, no need to re-compute
void do_update(size_t begin, size_t end) {
for (size_t c1 = begin; c1 < end; c1++) {
double d0 = mat(rstart - 1, c1);
double d1 = mat(rend - 1, c1);
sum[c1] += -d0 + d1;
sum2[c1] += -pow(d0, 2) + pow(d1, 2);
rmat(rend - 1, c1) = sqrt((sum2[c1] - pow(sum[c1], 2) / nwindow) / nwindow1);
}
}
// main entry -function call operator that work for the specified range (begin/end)
void operator()(size_t begin, size_t end) {
if (first_run)
do_first_run(begin, end);
else
do_update(begin, end);
}
};
// [[Rcpp::export]]
NumericMatrix cp_run_sd(NumericMatrix mat, int nwindow) {
// allocate the matrix we will return
int nc = mat.ncol();
int nperiod = mat.nrow();
NumericMatrix rmat(nperiod, nc);
// pad the first n-1 elements with NA
for (int i = 0; i < nc; i++)
fill_n(rmat.begin() + i*nperiod, nwindow - 1, NA_REAL);
// pre-compute first run
NumericVector rsum(nc), rsum2(nc);
run_sd_helper p(mat, 0, nwindow, rsum, rsum2, rmat);
parallelFor(0, nc, p);
// for loop for each time period in parallel
for (int i = 1; i < (nperiod - nwindow + 1); i++) {
// update stats
p.update(i);
parallelFor(0, nc, p);
}
return rmat;
}Please save above code in the runsd.cpp file or download runsd.cpp.
#*****************************************************************
# Compile Rcpp helper function to compute running window standard deviation in parallel
#*****************************************************************
# make sure to install [Rtools on windows](http://cran.r-project.org/bin/windows/Rtools/)
load.packages('Rcpp')
load.packages('RcppParallel')
sourceCpp('runsd.cpp')
tic(1)
sd252 = cp_run_sd(ret, 252)
toc(1)Elapsed time is 0.98 seconds
The Rcpp helper function took less than a second. This is an improvement i was lookin for.
Next, let’s address the run time for making back-test for each quantile. Please notice that instead of lagging and back-filling weights for each quantile, we can do it once to save time.
Following is final code that runs in about 28 seconds.
# https://systematicinvestor.wordpress.com/2012/06/05/volatility-quantiles/
#*****************************************************************
# Load historical data
#*****************************************************************
library(SIT)
load.packages('quantmod')
tic(2)
tic(1)
n = 25 * 1000
#n = 250
nperiods = 10 * 252
# force high vol to small return
library(MASS)
mu = c(5,20) / 100
sigma = c(5,10) / 100
rho = -0.9
cov.matrix = sigma%*%t(sigma) * matrix(c(1,rho,rho,1),2,2)
temp = mvrnorm(n, mu, cov.matrix)
mu = temp[,1]
sigma = temp[,2]
sigma[sigma < 1/100] = 1/100
ret = matrix(rnorm(n*nperiods), nr=n)
ret = t(ret * sigma/sqrt(252) + mu/252)
#colnames(ret) = paste('A',1:n)
dates = seq(Sys.Date()-nperiods+1, Sys.Date(), 1)
#prices = bt.apply.matrix(1 + ret, cumprod)
#plot(prices[,1])
#*****************************************************************
# Create Quantiles based on the historical one year volatility
#******************************************************************
period.ends = endpoints(dates, 'weeks')
period.ends = period.ends[period.ends > 0]
# compute historical one year volatility
toc(1); tic(1) Elapsed time is 6.85 seconds
if(F) { # 48 seconds
sd252 = bt.apply.matrix(ret, runSD, 252)
}
if(F) { # 38 seconds
# Run Cluster - will be about 10sec faster, please note transferring ret matrix takes almost 17secs
load.packages('parallel')
cl = setup.cluster(NULL, 'ret',envir=environment())
out = clusterApplyLB(cl, 1:n, function(i) { runSD(ret[,i], 252) } )
stopCluster(cl)
sd252 = do.call(c, out)
dim(sd252) = dim(ret)
}
if(T) { # 0.9 seconds
sd252 = cp_run_sd(ret, 252)
}
toc(1); tic(1) Elapsed time is 0.86 seconds
#all(abs(sd252 - result) < 0.0001, na.rm=T)
# split stocks into Quantiles using one year historical Volatility
n.quantiles=5
start.t = which(period.ends >= (252+2))[1]
quantiles = weights = ret[period.ends,] * NA
for( t in start.t:len(period.ends) ) {
i = period.ends[t]
factor = sd252[i,]
ranking = ceiling(n.quantiles * rank(factor, na.last = 'keep','first') / count(factor))
quantiles[t,] = ranking
weights[t,] = 1/tapply(rep(1,n), ranking, sum)[ranking]
}
quantiles = ifna(quantiles,0)
toc(1); tic(1)Elapsed time is 11.4 seconds
# free memory
env.del(spl('prices,sd252'), globalenv())
gc(T) used (Mb) gc trigger (Mb) max used (Mb) Ncells 637966 34.1 1073225 57.4 1012438 54.1 Vcells 208010169 1587.0 518657040 3957.1 518656088 3957.1
#*****************************************************************
# Create backtest for each Quintile
#******************************************************************
models = list()
weight = weights
# Simplified bt.run for speed
index = ret[,1] * NA
index[period.ends] = 1:len(period.ends)
index = ifna(ifna.prev(mlag(index)), 1)
for( i in 1:n.quantiles) {
weight[] = 0
weight[quantiles == i] = weights[quantiles == i]
rets = rowSums(ret * weight[index,])
models[[ paste('Q',i,sep='_') ]] = list(
ret = make.xts(rets, dates),
equity = make.xts(cumprod(1 + rets),dates))
}
gc(T) used (Mb) gc trigger (Mb) max used (Mb) Ncells 638113 34.1 1073225 57.4 1012438 54.1 Vcells 154037802 1175.3 414925632 3165.7 518656088 3957.1
toc(1); tic(1)Elapsed time is 9.17 seconds
#*****************************************************************
# Report
#*****************************************************************
#strategy.performance.snapshoot(models, T)
plotbt(models, plotX = T, log = 'y', LeftMargin = 3, main = NULL)
mtext('Cumulative Performance', side = 2, line = 1)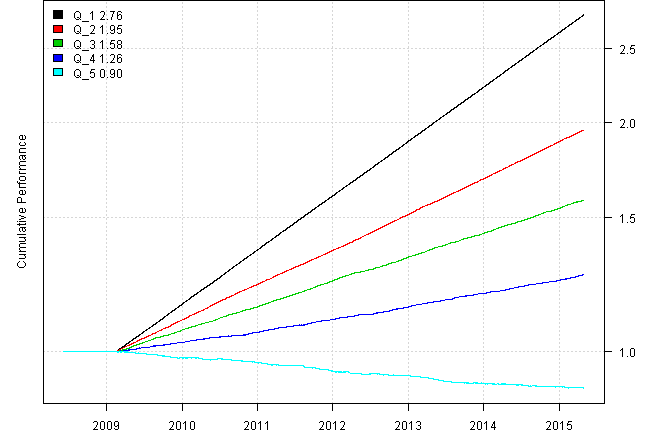
toc(1); Elapsed time is 0.03 seconds
toc(2); Elapsed time is 28.31 seconds
Aside: Rcpp helper function testing:
#*****************************************************************
# Compile Rcpp helper function to compute running window standard deviation in parallel
#*****************************************************************
# [RcppParallel help site](http://rcppcore.github.io/RcppParallel/)
# [RcppParallel source code](https://github.com/RcppCore/RcppParallel)
# [RcppParallel introduction](http://dirk.eddelbuettel.com/blog/2014/07/16/#introducing_rcppparallel)
# [RcppParallel gallery](http://gallery.rcpp.org/articles/parallel-distance-matrix/)
# defaultNumThreads()
#[High performance functions with Rcpp](http://adv-r.had.co.nz/Rcpp.html)
#
# make sure to install [Rtools on windows](http://cran.r-project.org/bin/windows/Rtools/)
load.packages('Rcpp')
load.packages('RcppParallel')
sourceCpp('runsd.cpp')
# test - generate random data
n = 24
nperiods = 10 * 252
ret = matrix(rnorm(n*nperiods), nc=n)
# compute running window standard deviation using Rcpp
cp.sd252 = cp_run_sd(ret, 252)
# compute running window standard deviation using R
library(SIT)
load.packages('quantmod')
r.sd252 = bt.apply.matrix(ret, runSD, 252)
print(test.equality(r.sd252, cp.sd252))| item1 | item2 | equal |
|---|---|---|
| r.sd252 | cp.sd252 | TRUE |
# compare performance
library(rbenchmark)
res <- benchmark(
cp_run_sd(ret, 252),
bt.apply.matrix(ret, runSD, 252),
replications = 20,
order="relative")
print(res[,1:4])| rownames(x) | test | replications | elapsed | relative |
|---|---|---|---|---|
| 1 | cp_run_sd(ret, 252) | 20 | 0.16 | 1.000 |
| 2 | bt.apply.matrix(ret, runSD, 252) | 20 | 0.94 | 5.875 |
(this report was produced on: 2015-05-01)